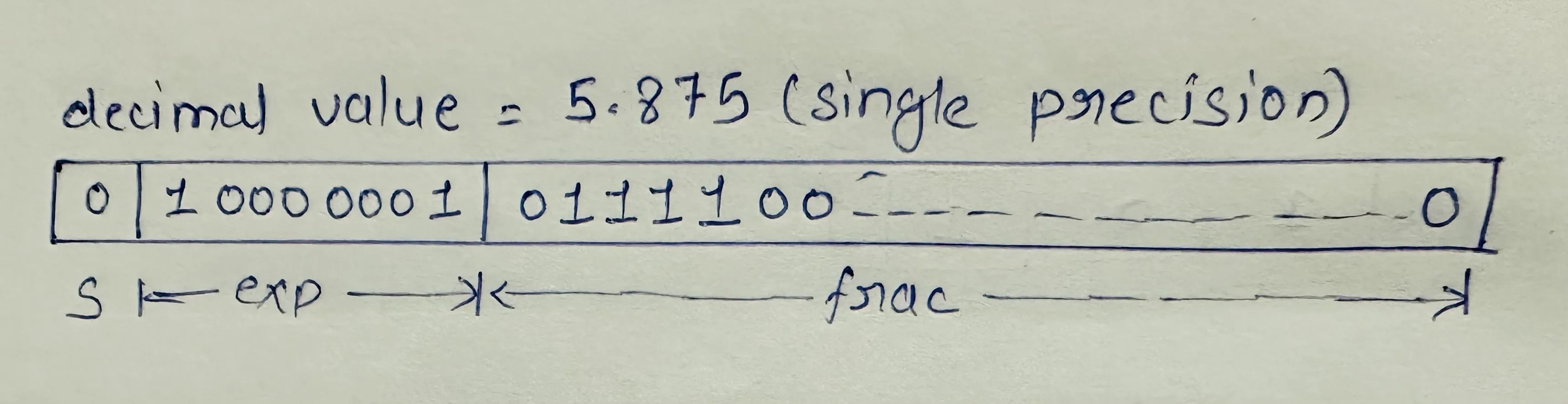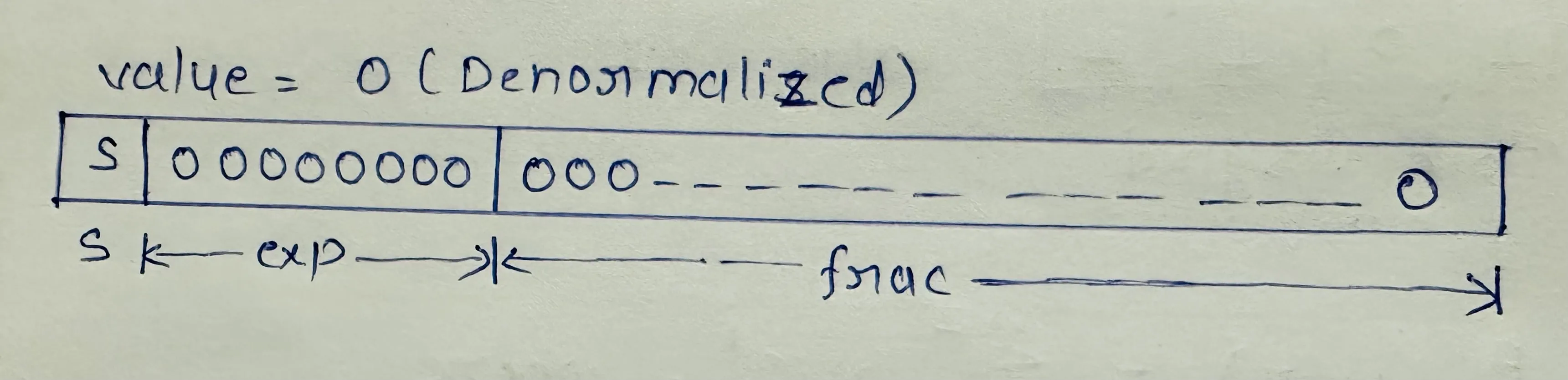How Floating Points Are Stored in Memory

The computer can only understand binary patterns, i.e., sequences of binary numbers. These binary patterns can be identified as int, char, float, double, or others, and programmers decide what these patterns mean. This way of interpreting binary patterns is called encoding or data representation. Integers (positive or negative) are relatively easy to represent, and I have discussed them here. However, representing real numbers with fractional parts is somewhat complicated. This binary representation can be used for very small numbers (approximating zero) or very large numbers and is useful for performing computations. 

Integer representations can encode a comparatively small range of values but do so precisely, while floating-point representations can encode a wide range of values but only approximately. 

Data Representation

Any real number can be represented as:

`F * (radix)^E` where

F => fractional part

E => exponent; it is signed

radix => representation pattern, 2 for binary, 10 for decimal, etc.

Since computers have fixed sizes, not all numbers can be represented. It is limited by 32-bit float or 64-bit double in C (and other programming languages). Hence, there is an approximation, which leads to a loss of precision. Floating point arithmetic is significantly less efficient than integer arithmetic.

Floating Point Representation

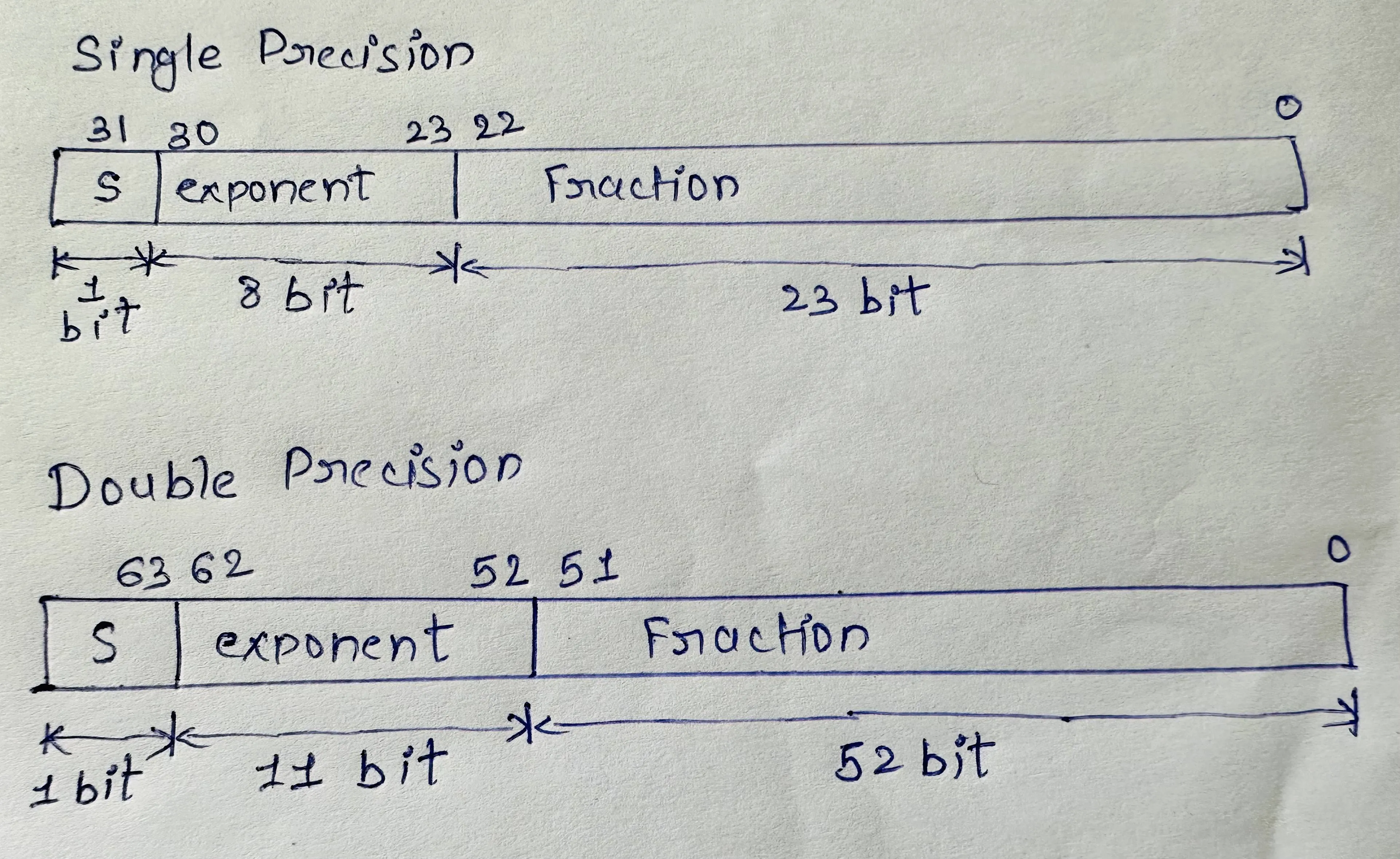
Virtually all computers today follow the IEEE Standard 754 for representing and computing floating point numbers. As per the IEEE standard, the binary representation of a floating point number is divided into three fields (shown in the figure below) and is represented as:

V = (-1)^s * M * 2^E

Here, s, E, and F represent:

S => Sign. This is 1 bit, 0 for positive numbers, and 1 for negative ones.

E => Exponent. This is 8 bits for 32-bit data type and 11 bits for 64-bit.   

M => Fractional part or Mantissa, i.e., the number after the radix point. This is 23 bits for 32-bit data type and 52 bits for 64-bit.

32-bit (Float) and 64-bit (Double Precision) Binary representation

Biasing

In memory space, the exponent bits are represented as unsigned numbers, but as per the standard, it's a signed number. So, to convert unsigned to signed, we subtract the bias from the exponent while converting binary representation into a numeric value.

Actual exponent (E) = e - bias, where

e => unsigned number represented in bit form 

bias => 2^(w-1) - 1, for 8-bit number bias is 127.

Normalised Form

This is the most common case. This form represents values that do not have all 0s (numeric value 0) nor all ones (numeric value 2^w - 1 for w-bit number). The leading bit 1 is added to the fractional part or mantissa. Thus, the above formula changes to 

V = (-1)^s * (1 + F) * 2^(e - bias)

For example, consider a decimal value 5.875 which can be represented in binary memory space as in the diagram below.

Thus, the above number (5.875D) in a single precision float can be represented in binary form (memory space) as: 

This form adds 1 bit of precision and eliminates the need to store the leading bit 1 in memory. The exponent is adjusted so that M always falls between 1 and 2.

This form cannot represent zero or very small numbers between (0 and 1). Thus, we use the denormalized form for this.

Denormalised Form

This form represents zero or very small numbers between 0 to 1. Here, the leading bit is always zero i.e. M = f. 

The formula for converting binary representation to actual number is

V = (-1)^s * (F) * 2^(e - bias)

Thus, zero can be represented in memory bit representation as: 

Sources

Book - Computer Systems: A Programmer's Perspective