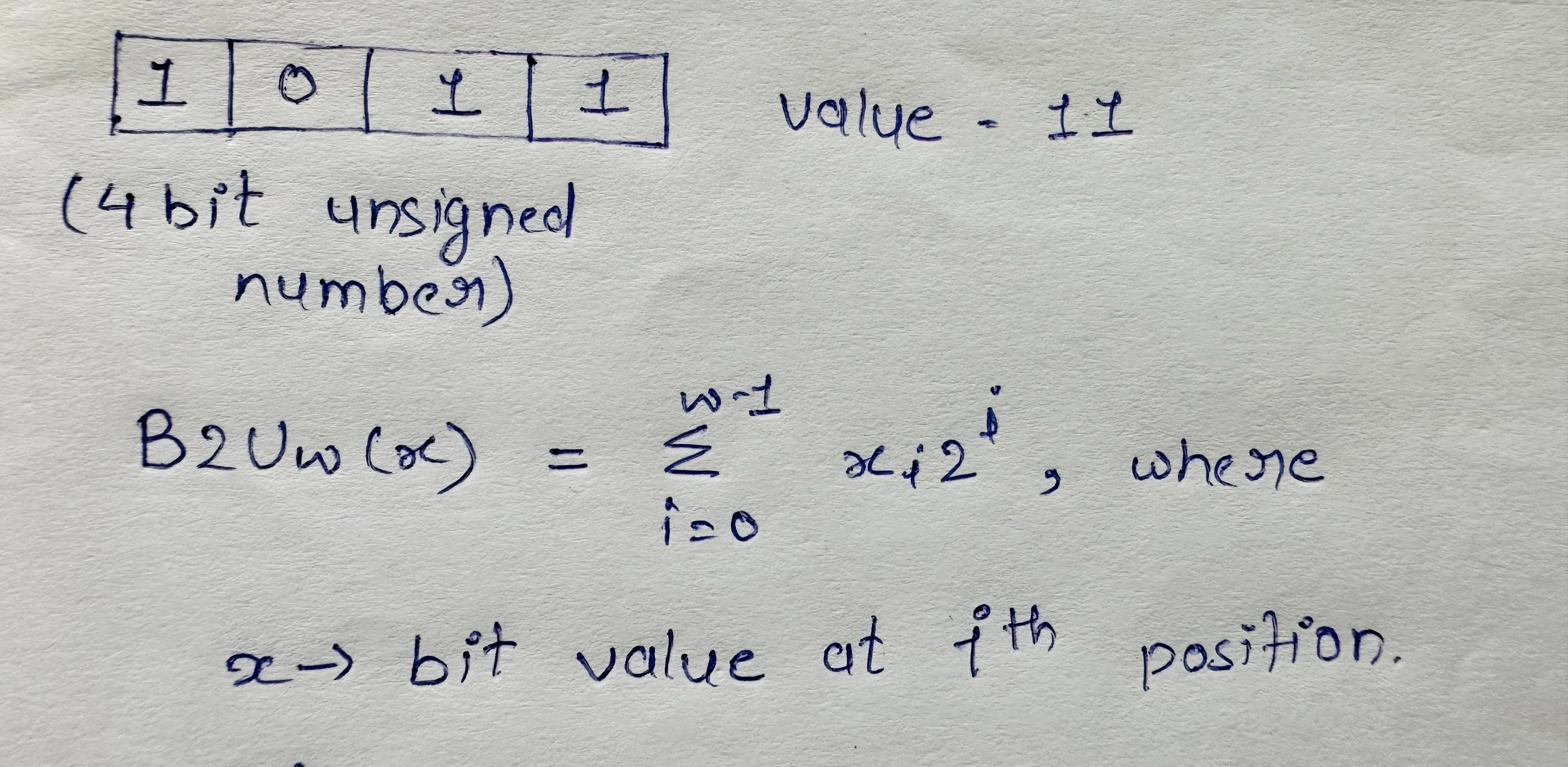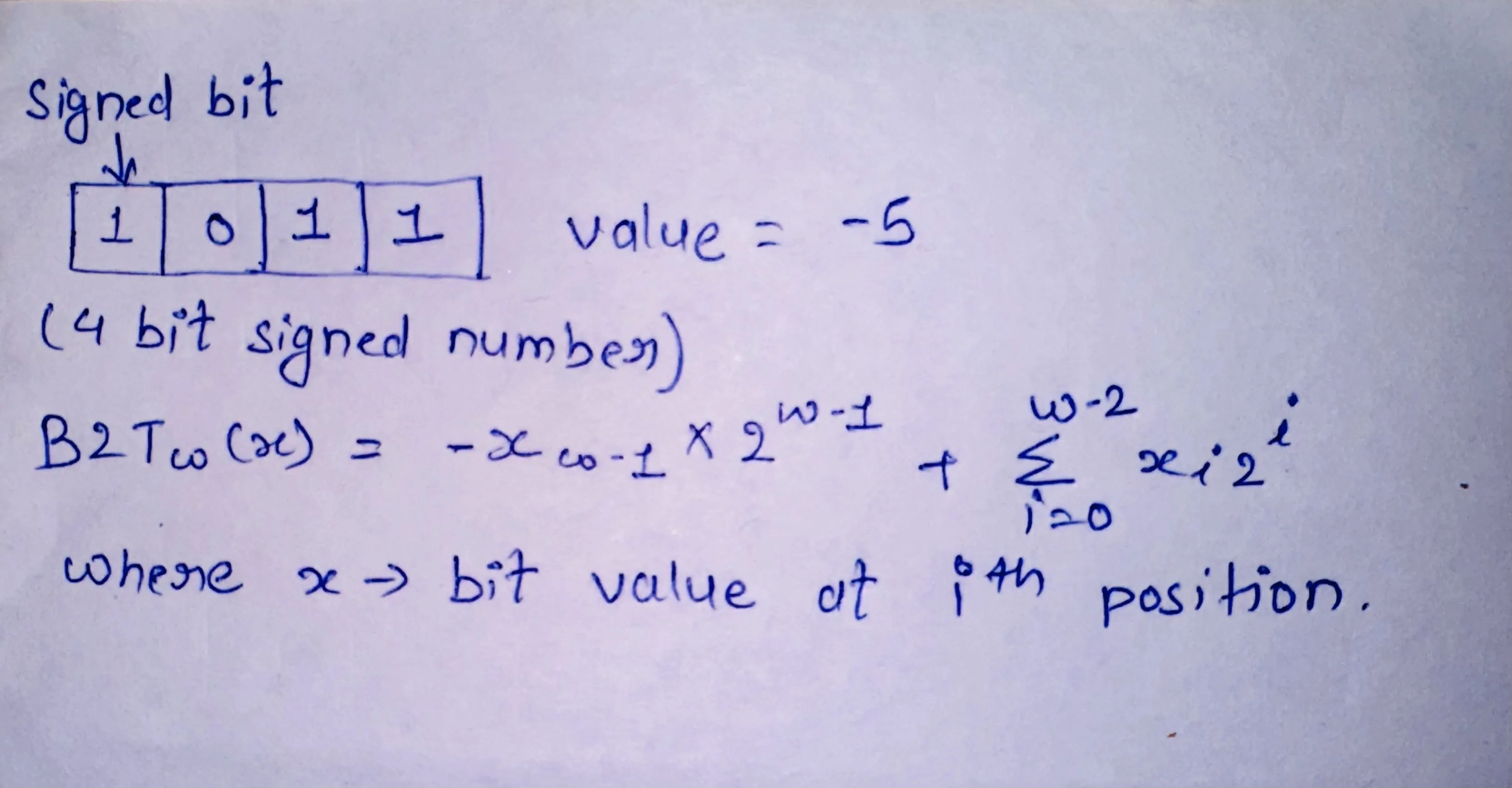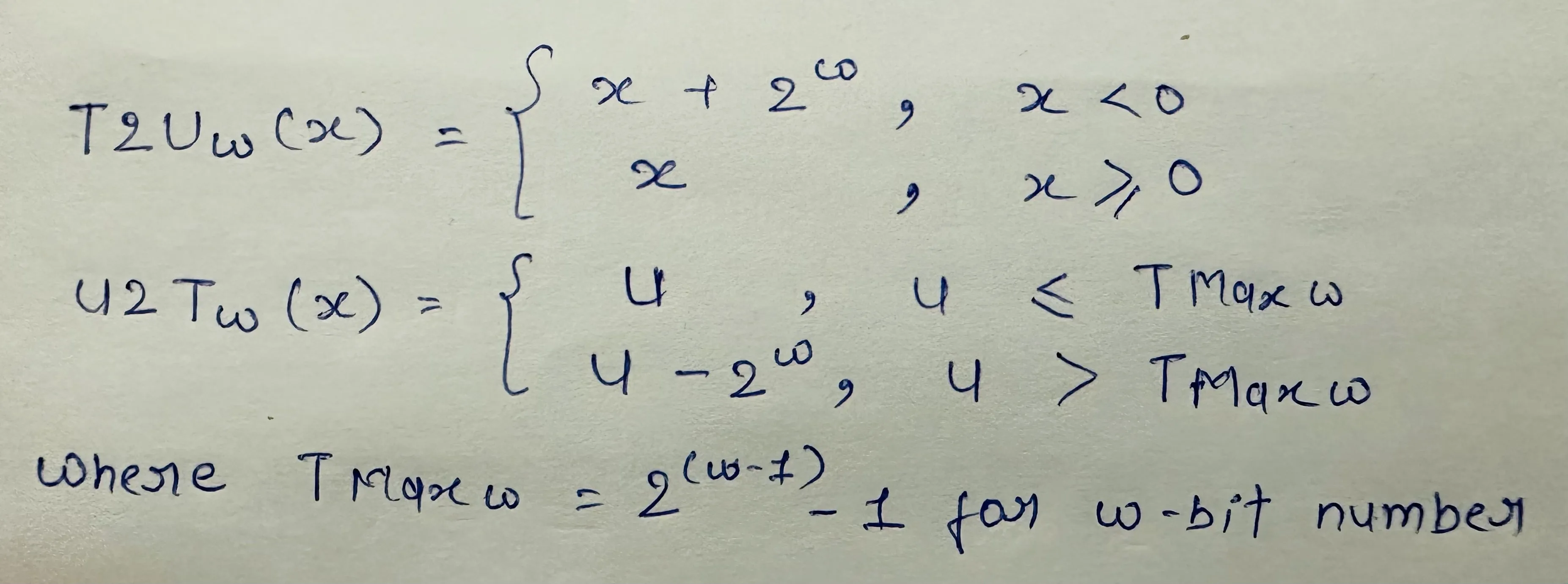December 13, 2023
How Integers Are Stored in Memory
Computers store and process information in patterns of binary sequences, i.e., 0 or 1. Thus, these sequences can represent numbers, characters, or others. It is up to the programmer to decide what information should be interpreted from x-bit binary sequences. This interpretation of information from binary patterns is called encoding or data representation.
There are three main representations of numbers. Unsigned encodings are used to represent non-negative integers or integers >= 0, Two's complement encodings are used to represent signed integers, i.e., positive, negative, or zero, and Floating point encodings are used to represent real numbers. We will discuss the first two in this article, and floating point encoding is discussed here.
Binary Representation
Unsigned Encodings
In unsigned encoding, all bits 0 or 1 will contribute to calculating the numeric value, i.e., ith bit with value 1 adds 2^i to the numeric value. Hence, integer values that can be represented using w-bit size are 0 to 2^w - 1, also called UMax. For example, the min and max integers represented by 8 bits are 0 and 255, respectively.
We can express the above interpretation using a function B2U, i.e., Binary to Unsigned, below, for calculating the range of values for a w-bit number.
Unsigned encoding has one important property: every number between 0 and 2^w - 1 will have a unique encoding as a w-bit value.
Two's Complement Encodings
This is the most common representation of signed integers. Here, the most significant bit (MSB) represents the sign of an integer. Thus, if MSB is 1, it represents a negative value, and 0 represents a positive value. All the other bits contribute to calculating the numeric value. Hence, integer values that can be represented using w-bit size range from -2^(w-1), called TMin to 2^(w-1) - 1, called TMax. For example, the min and max integers represented by 8 bits are -128 and 127, respectively.
All bit patterns of w-bit from TMin to TMax have unique w-bit encodings, just like unsigned encodings.
Conversion between Signed and Unsigned
The standard practice for most C implementations when casting between signed and unsigned integers of the same word size is that the bit patterns should not change, while numeric values can change. In two's complement, the MSB is the signed bit. When converting from signed to unsigned, add 2^w if the MSB is 1. When converting from unsigned to signed, subtract 2^w if the MSB is 1. I have added the formula below.
The formula for converting a w-bit signed number to an unsigned number is represented by T2Uw(x) and U2Tw(x) and vice versa. Here, x represents the bit value at the ith position.
Signed Unsigned Conversion in C
- C standard does not specify a particular representation of -ve numbers, but most machines implement Two's complement encoding.
- In C, integers are signed by default. To represent the integer as unsigned, use the U suffix. Example: 978U while 978 is signed.
- When an operation is performed between signed and unsigned numbers, the signed number is implicitly cast to an unsigned number, and the operation is performed as if both numbers were unsigned. This is fine for arithmetic operations but fails in cases of comparisons. In the expression "-1 < 0U", -1 is converted from signed to unsigned, resulting in 2^32 - 1 (int in C is 4 bytes, i.e. w=32). Therefore, the expression yields an incorrect result.
Expanding bit representation of Number (32 bit to 64)
One common operation of integer is to have same numeric value for data type of different word sizes. This is only possible if the destination type is a larger data type i.e. from int to long, etc.
To convert an unsigned number to a larger data type, add leading zeroes to binary representation. This is called zero extension.
To convert signed number to a larger data type, add copies of MSB to the binary representation. This is called sign extension.
For example, for converting 4-bit unsigned number i.e. 1011 to 8-bit number result in 00001011
Common Integer Sizes
Typically, integers are stored using a fixed number of bits, i.e., fixed-size data, which is determined using data type declaration. This guarantees that there will always be a fixed range of values that a particular data type can represent.
Common integer sizes include 8-bit, 16-bit, 2-bit, and 64-bit representations. The number of bits determines the range of values that the integer can represent. For example, an 8-bit integer can represent values from 0 to 255, while a 2-bit integer can represent values from -2,147,48,648 to 2,147,48,647 in the case of signed integers.
Endianness
For objects like integers in C that span multiple bytes, we need two conventions to define the location of that object in memory. First, what is the address of bytes, and second order of the bytes in which they are stored in memory? First, machines represent the address of multiple objects as a contiguous sequence of bytes (block of 8 bits). While, the order in which bytes are stored might vary from machine to machine. Systems that store the least significant byte first are called little-endian, and systems that store the most significant byte are called big-endian. Endianness can affect the way integers are stored and manipulated.